BOLD decoding with RKRNS

Introduction

RKRNS Algorithms

This package integrates several frameworks for BOLD processing:

  • core image processing and I/O: ITK (Avants, Tustison, et al. (2014));

  • registration and utilities for image processing: ANTs (Tustison et al. (2014)) and ANTsR (PICSL (2014));

  • hemodynamic response function estimation: influenced by GLMdenoise (Kay et al. (2013)) and finite impulse response (Kay et al. (2008)) estimates;

  • dimensionality reduction: Eigenanatomy (Dhillon et al. (2014)) and SCCAN (Avants, Libon, et al. (2014));

  • core statistics and temporal filtering via R packages.

In combination, these tools enable one to go from near-raw medical imaging data to a BOLD decoding experiment.

Data organization expected by RKRNS

RKRNS makes several assumptions about data organization.

  • The BOLD time series will be masked and converted to a matrix. This will be known as “the BOLD matrix.”

  • The design matrix is binary and has one event type per column.

  • The design matrix matches the bold matrix in time at an index level. Thus, it has the same number of rows (volumes) as the BOLD matrix. So, the i\(^{th}\) row of the design matrix corresponds to the i\(^{th}\) BOLD volume. We provide some utilities to assist in assembling the BOLD volumes in this manner.

  • Simplicity aids debugging but has caveats (rounded event onsets, etc).

Contributions of the package

RKRNS includes:

  • An organizational system

  • relatively small scripts implement full study

  • Implementation of foundational methods
  • HRF estimation
  • event-wise \(\beta\) estimation
  • denoising via compcor and glmDenoiseR

  • flexible: easy to estimate voxel-wise optimal models, HRFs, etc

  • Reference simulation data and decoding distributed with the package

  • Interpretation of results
  • sparse low-dimensional predictors

  • anatomical labeling of predictors based on AAL

  • Openness and reproducibility

  • this document tests the package

Decoding in simulated data

Example BOLD Data

We adapted methods from the neuRosim (Welvaert et al. (2011)) package in order to simulate event-related BOLD data. This data involves a 4-class decoding task. One seeks to identify brain responses to novel faces, famous faces and their first and second presentations to the subject. We distribute the underlying anatomical BOLD data along with a cortical mask within the package. The data may be loaded by:

library(RKRNS)
fn<-paste(path.package("RKRNS"),"/extdata/111157_mocoref_masked.nii.gz",sep="") 
eximg<-antsImageRead(fn,3)
fn<-paste(path.package("RKRNS"),"/extdata/subaal.nii.gz",sep="") 
mask<-antsImageRead(fn,3)

which gives you both the cortical mask and the example BOLD signal image eximg. ANTsR also provides AAL label (Tzourio-Mazoyer et al. (2002)) names via:

data(aal,package='ANTsR')
labs<-1:90

with cortical labs defined by labs.

Run the simulation

We generate simulated bold data as in neuRosim.
The simulateBOLD function results in a bold image in the antsImage class. We subsequently convert this image to a \(n\times p\) matrix where there are \(n\) time volumes and \(p\) voxels in the mask.

bb<-simulateBOLD(option="henson",eximg=eximg,mask=mask)
boldImage<-bb$simbold
mat<-timeseries2matrix( boldImage, bb$mask )

The data frame containing the bold image also contains the design matrix. One should inspect that matrix to get an idea of the structure expected by RKRNS. Row names and column names are expected to exist in the design matrix dataframe.

Simulated BOLD time series

Perform some diagnostic visualizations on the data.

randvox<-sample(1:ncol(mat),4)
plot(ts(mat[,randvox]))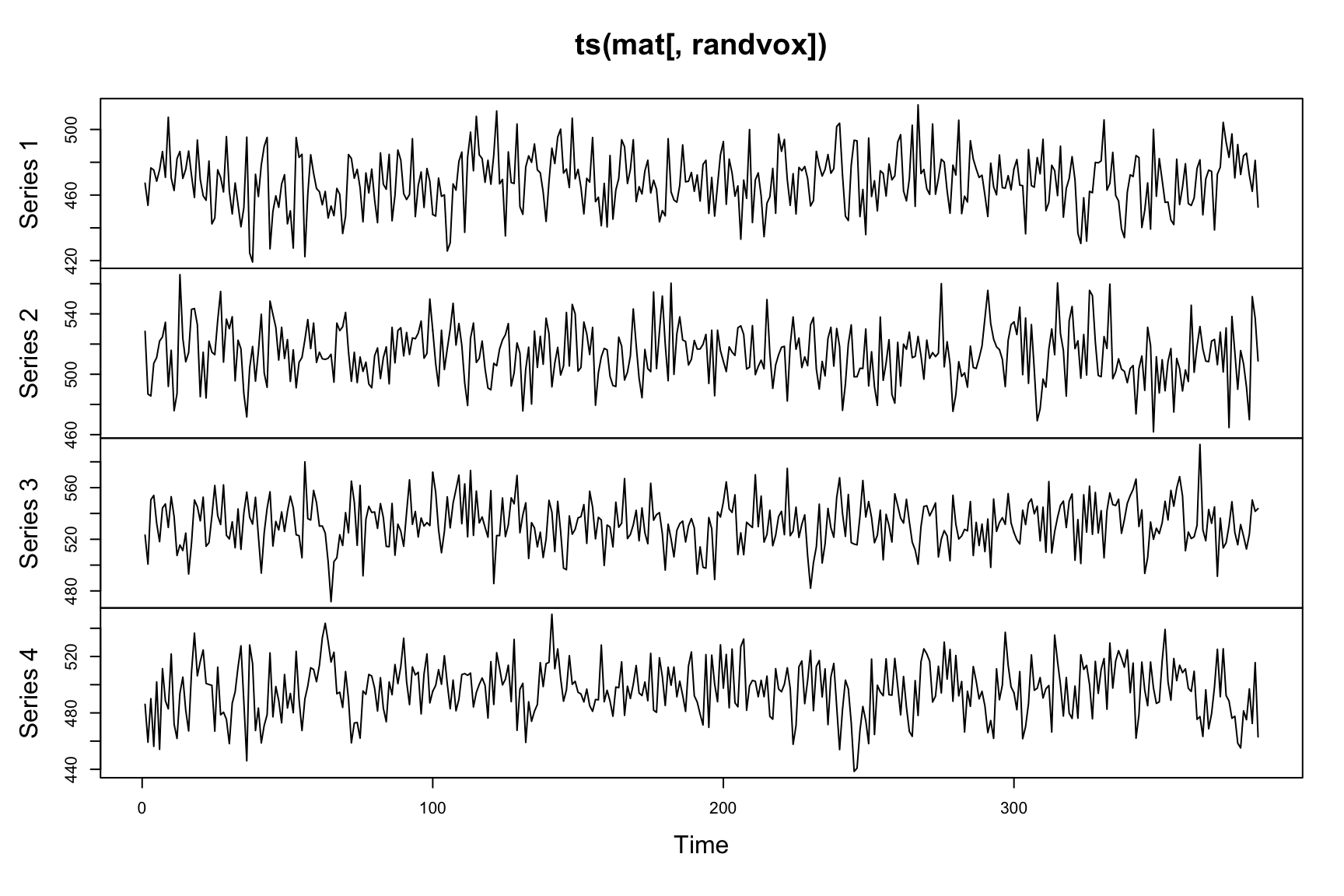

plot of chunk simbviz The time series is noisy, as expected.

Frequency filtering

Let’s get rid of high frequency noise.

# only filter high frequencies 1/(2*tr)
filtmat<-filterfMRI4KRNS( data.matrix(mat), tr=1, NA, NA, trendfrequency=2, trendfrequency2=NA )
plot(ts(filtmat[,randvox]))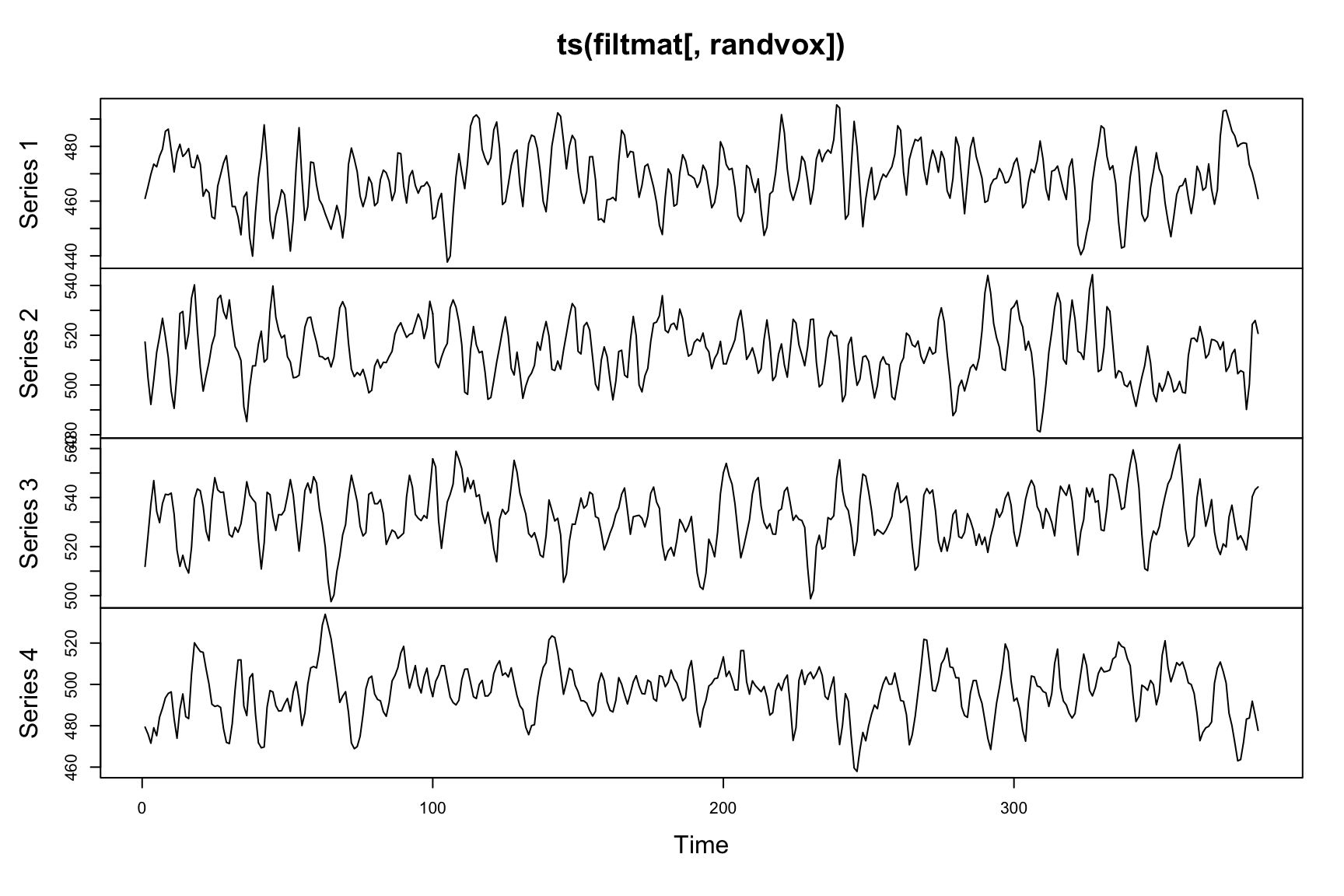

plot of chunk ffilt We can eliminate low frequency contamination with polynomial regressors and other denoising techniques at a later step.

Autoregression Correction

armat<-arCorrection( mat )
print(armat$arcoefs)
## [1] -0.02820 -0.05086
plot(ts(armat$outmat[,randvox]))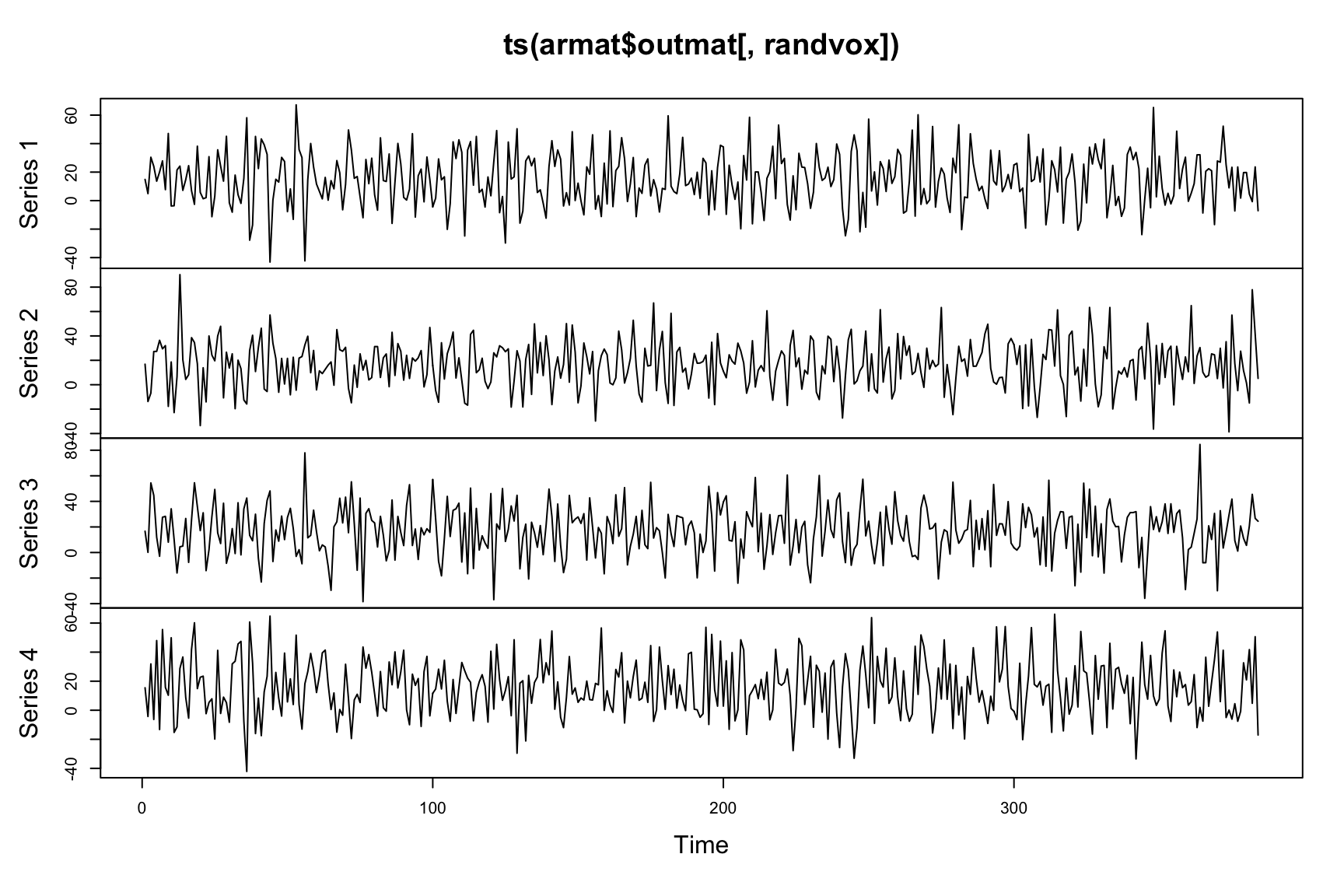

plot of chunk arfilt The armat$arcoefs indicate auto-correlation levels of the input data. This function tries to shrink these levels toward zero.

Estimate the hemodynamic response function

Use glmDenoiseR to estimate a FIR HRF.

mypolydegree<-12
glmda<-glmDenoiseR( data.matrix(mat), bb$desmat[,1:4], hrfBasis=NA, 
  hrfShifts = 12, maxnoisepreds=0 , selectionthresh=0.1 , 
  collapsedesign=T, polydegree=mypolydegree, baseshift=0 )

Visualize the HRF

Take a quick look at the estimated hemodynamic response function.

plot(ts(glmda$hrf))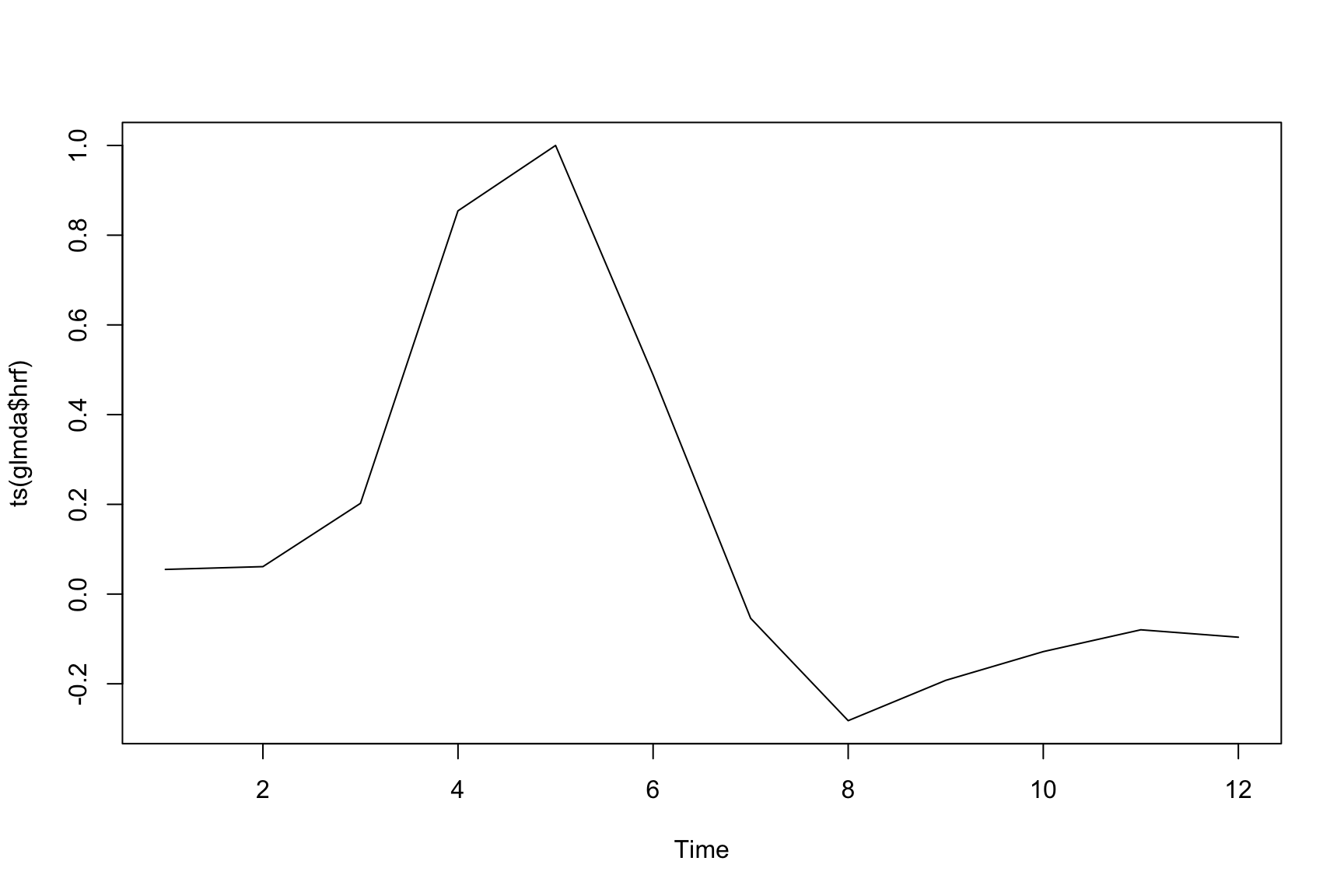

plot of chunk vizhrf If this doesn’t look “normal,” then there may be a problem. One might also do an SVD on the run-wise HRFs and derive a more flexible basis set for your study.

Estimate \(\beta\) values for each event

We estimate a \(\beta^i\) vector for each of \(i \in 1 \cdots q\) events. This vector contains a scalar \(\beta\) value for each voxel, i.e. \(\beta_j^i\) where \(j \in 1 \cdots p\). This example can be found via ?bold2betas.

runs<-bb$desmat$Run; 
btsc<-bold2betas( boldmatrix=data.matrix(mat), 
      designmatrix=bb$desmat[,1:4], baseshift=0,
      blockNumb=runs, maxnoisepreds=0, hrfBasis=glmda$hrf,
      hrfShifts=0, polydegree=mypolydegree, selectionthresh=0.2 )
mylabs<-rep("",nrow(btsc$eventbetas))
for ( i in 1:nrow(btsc$eventbetas) ) 
  mylabs[i]<-substr( rownames(btsc$eventbetas)[i],1,2)
mylabs<-as.factor(mylabs)

Estimate \(\beta\) values for each event: 2

We recommend that one looks at the estimated hemodynamic response function in order to help set parameters. This is available as output from the bold2betas function (and glmDenoiseR). Key parameters are the basis length for HRF estimation, the maximum number of noise predictors (e.g. maxnoisepreds=4 or maxnoisepreds=2:10 to search a range), the polynomial degree and the selectionthresh which should be kept below 0.5. Real data processing should proceed similarly. The latter part of the sample code extracts labels from the rownames of the output event beta dataframe. This will set us up for decoding.

Decode from event-wise \(\beta\)

Use effect size to select a subset of the full voxel matrix.

# sample for training
inds<-sample(1:nrow(btsc$eventbetas),size=round(nrow(btsc$eventbetas)*3./4.))
# basic voxel selection using effect size & classification
zz<-apply(btsc$eventbetas,FUN=mean,MARGIN=2)
zze<-zz/apply(btsc$eventbetas,FUN=sd,MARGIN=2)
th<-0.4
ff<-which( abs(zze) > th )
mydf<-data.frame( lab=mylabs,  vox=data.matrix(btsc$eventbetas)[,ff])
mdl<-svm( lab ~., data=mydf[inds,])
err<-sum(mydf[-inds,]$lab==predict( mdl, newdata=mydf[-inds,]))/nrow(mydf[-inds,])
print(paste("NPredVox",length(ff),"Correct",err*100))
## [1] "NPredVox 612 Correct 72"

The “high effect size” voxels are sent to a naive support vector machine to do training (on a fraction of the data) and testing on the left out data.

Cross-validated effect size

Effect size increases when a measurement has low variance and a high value. The effect size of cross-validated beta estimates may aid voxel selection.

# ccnuis<-compcor( mat, 2 ) # a denoising option not used here ....
stb<-stableEventResponse( mat,  bb$desmat[,1:4], bb$desmat$Run,  
            polydegree=mypolydegree, hrf=btsc$hrf )

Voxels of clustered effect size

Use a threshold to find clusters of voxels with large effect.

stb2<-abs(stb)
stb2[ stb2 < 5 ]<-0
ee<-eigSeg(mask, matrixToImages( stb2, mask) )
ImageMath(3,ee,'ClusterThresholdVariate',ee,mask,5)
ff<-which( ee[mask==1] > 0 )
ofn<-"Figs/eigseg.jpg"
plotANTsImage( eximg, list(ee), slices='12x56x1',
  thresh='1x4',color='red',outname=ofn)

The eigSeg function labels each region of the mask with the class that has the largest effect size.

Should return the magnitude of effects … FIXME colors above.

eigSeg Viz

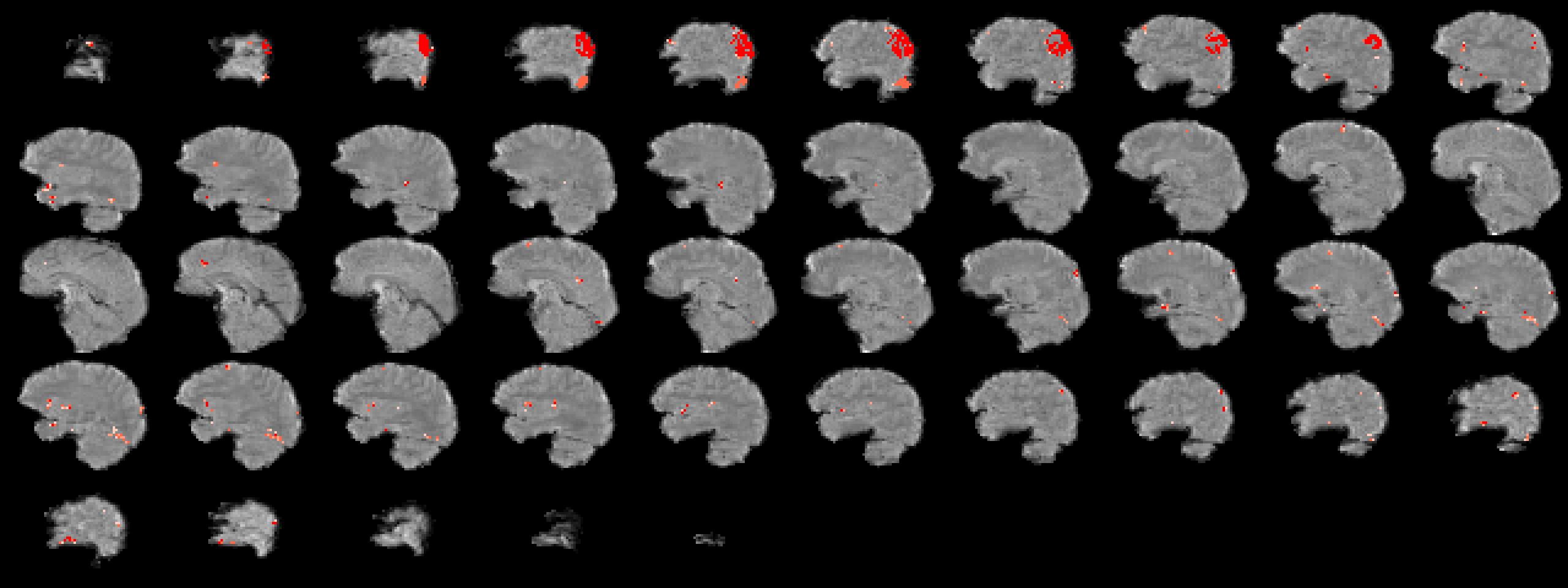
Decode with effect size clusters

Use only those voxels that exist within clusters and have maximum response for some label class.

mydf<-data.frame( lab=mylabs,  vox=data.matrix(btsc$eventbetas)[,ff])
mdl<-svm( lab ~., data=mydf[inds,])
err<-sum(mydf[-inds,]$lab==predict( mdl, newdata=mydf[-inds,]))/nrow(mydf[-inds,])
print(paste("EigSegPredVox",length(ff),"Correct",err*100))
## [1] "EigSegPredVox 753 Correct 80"

Time series per stimulus

Investigate the time series for each stimulus.

plot of chunk stimulusts

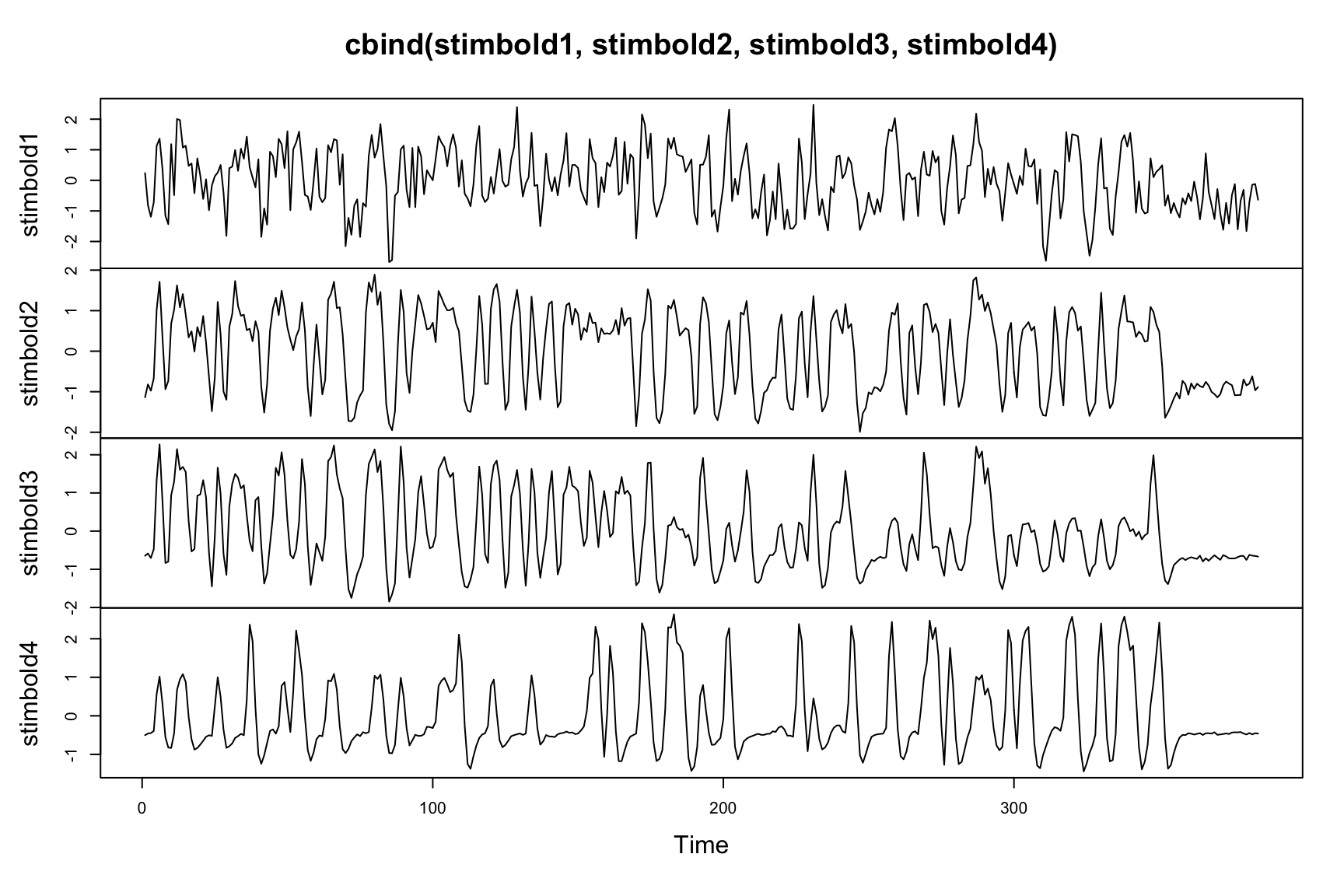
Sparse canonical correlation between BOLD and stimuli

CCA maximizes \(PearsonCorrelation( XW^T, ZY^T )\) where \(X, W\) are as above and \(Z\) and \(Y\) are similarly defined. CCA optimizes the matrices \(W, Y\) operating on \(X, Z\) to find a low-dimensional representation of the data pair \(( X , Z )\) in which correlation is maximal. Following ideas outlined in Dhillon et al. (2014) and Avants, Libon, et al. (2014), this method can be extended with sparsity constraints that yield rows of \(W, Y\) with a controllable number of non-zero entries.

SCCAN voxel selection & classification

Set up the CCA by pairing the beta matrix with the design matrix.

ccamats<-list( data.matrix(btsc$eventbetas)[inds,] , 
               data.matrix(bb$desmat[btsc$eventrows,1:4])[inds,] )

Initialize SCCAN

Use the SVD of the beta matrix to initialize sparse CCA.

initcca<-t( svd( btsc$eventbetas, nu=0, nv=10 )$v )
initcca<-initializeEigenanatomy( initcca, mask=mask, nreps=1 )$initlist
nv<-length(initcca)

These 10 vectors initialize the sparse optimizer in a good place.

Supervised clustering with SCCAN

The design matrix guides the dimensionality reduction performed on the \(\beta\) matrix.

mycca<-sparseDecom2( inmatrix=ccamats, initializationList=initcca,
  sparseness=c( -0.001, -0.95 ), nvecs=nv, its=10, cthresh=c(250,0),
  uselong=0, smooth=0.0, mycoption=1, inmask=c(mask,NA) )
ccaout<-(data.matrix(imageListToMatrix( mycca$eig1, mask )))
ff<-which(colSums(abs(ccaout))>1.e-4)

We also count the non-zero voxels which cover 0.787% of the brain.

Predictive model

Given CCA solution matrix \(W\), one may employ the low-dimensional representation, \(XW^T\), in multi-label classification. Currently, we employ SVM or random forests as multi-label learners for the problem:

\[L_i = f( XW^T ),\]

that is, learning a (sentence) label function from the BOLD data.

Predictive model: 2

mydf<-data.frame( lab=mylabs,  
  vox=data.matrix(btsc$eventbetas) %*% t(ccaout) )
mdl<-svm( lab ~., data=mydf[inds,])
err<-sum(mydf[-inds,]$lab==predict( mdl, newdata=mydf[-inds,]))/nrow(mydf[-inds,])
print(paste("CCA: Correct",err*100))
## [1] "CCA: Correct 80"
# here is another approach ... use cca to transform BOLD signal to stimuli 
mydf3<-data.frame( lab=mylabs, 
  vox=data.matrix(btsc$eventbetas) %*% t(ccaout) %*% t(mycca$eig2) )
mdl2<-svm( lab ~., data=mydf3[inds,])
err<-sum(mydf3[-inds,]$lab==predict( mdl2, newdata=mydf3[-inds,]))/nrow(mydf3[-inds,])
print(paste("CCA2: Correct",err*100))
## [1] "CCA2: Correct 84"

The input predictors are both clustered and sparse.

Quick look at CCA results

Rescale the cca results and make a picture.

CCA results in image space

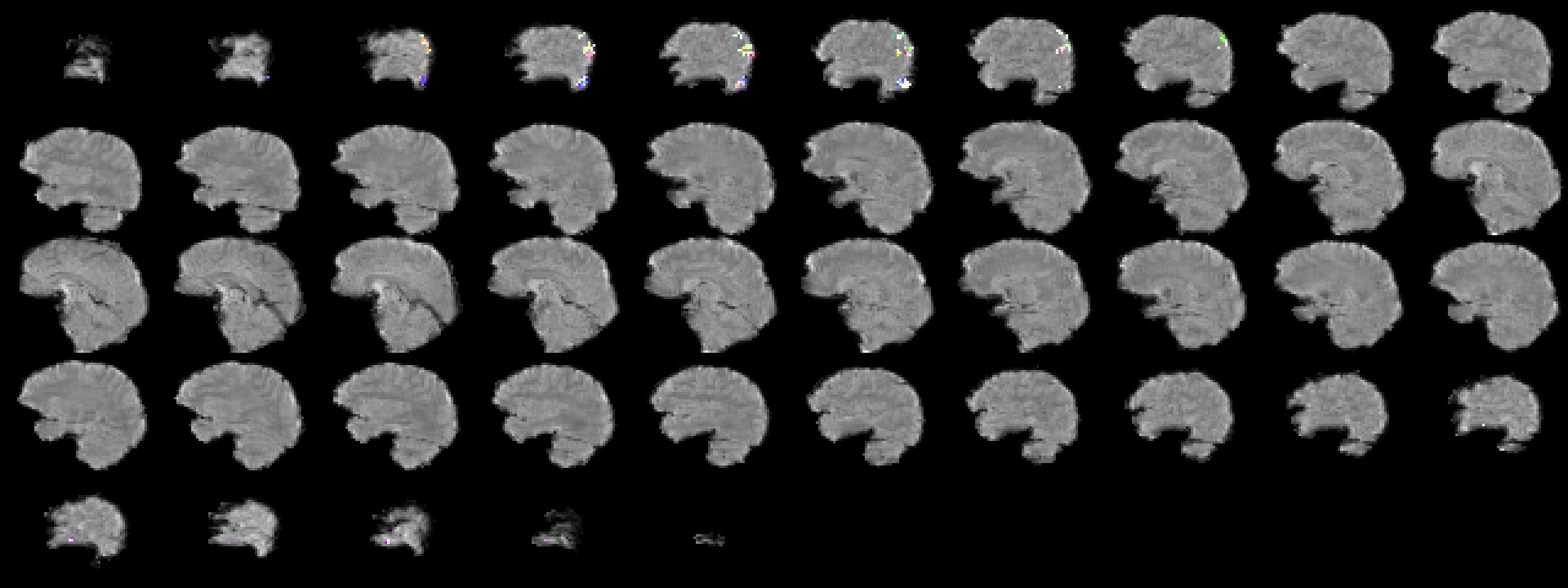
Interpreting SCCAN results

Confusion matrix

heatmap of co-occurrence of predictions

##     truth
## pred F1 F2 N1 N2
##   F1  5  0  1  1
##   F2  1  5  0  1
##   N1  0  0  2  1
##   N2  0  0  0  8

Confusion matrix 2

plot of chunk confmat2

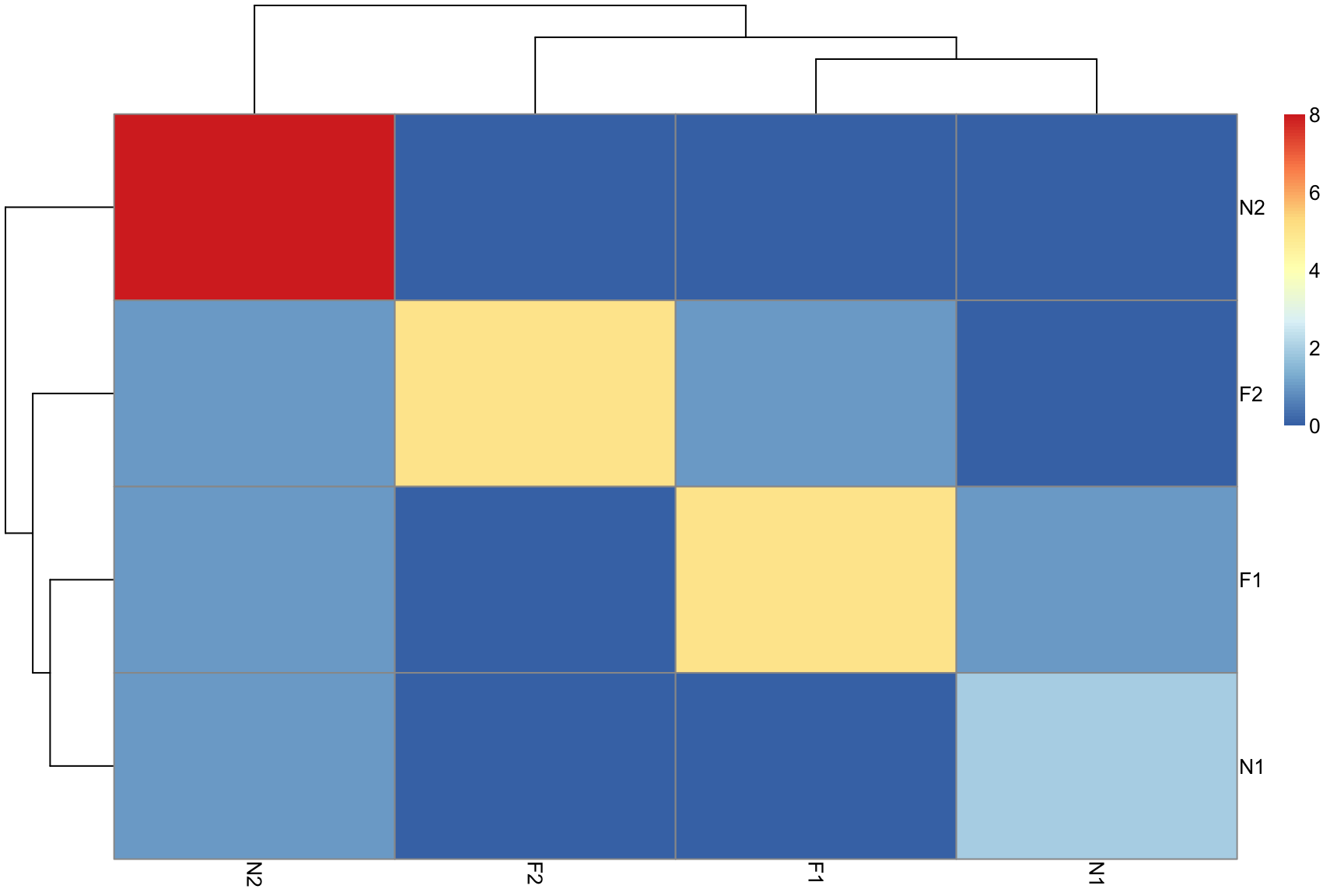
Anatomical coordinates of SCCAN predictors

ANTs propagates AAL labels to the cortex (Avants, Tustison, et al. (2014),Tustison et al. (2014))

fn<-paste(path.package("RKRNS"),"/extdata/111157_aal.nii.gz",sep="") 
aalimg<-antsImageRead(fn,3)
ccaanat<-list()
for ( img in mycca$eig1 ) {
  nzind<-img[ mask == 1 ] > 0 
  aalvals<-aalimg[ mask == 1 ][ nzind ]
  aalmax<-which.max( hist( aalvals, breaks=1:90, plot=FALSE )$counts )+1 
  ccaanat<-lappend( ccaanat, aal$label_name[aalmax] )
}

The SCCAN predictors include: Temporal_Inf_R, Temporal_Inf_R, Angular_R, Angular_R, Parietal_Inf_R, Temporal_Inf_R, Temporal_Inf_R, Temporal_Inf_R, Temporal_Inf_L, Angular_R.

How much of the known network do we actually find?

Associating classes to SCCAN predictors

Recalling: CCA maximizes \(PearsonCorrelation( XW^T, ZY^T )\), we can study matrix \(Y\) which contrasts or combines columns of the design matrix.

rownames(mycca$eig2)<-levels(mylabs)
temp<-(mycca$eig2)
temp[ abs(mycca$eig2) < 0.03 ]<-0

Associating classes to SCCAN predictors: 2

pheatmap(temp)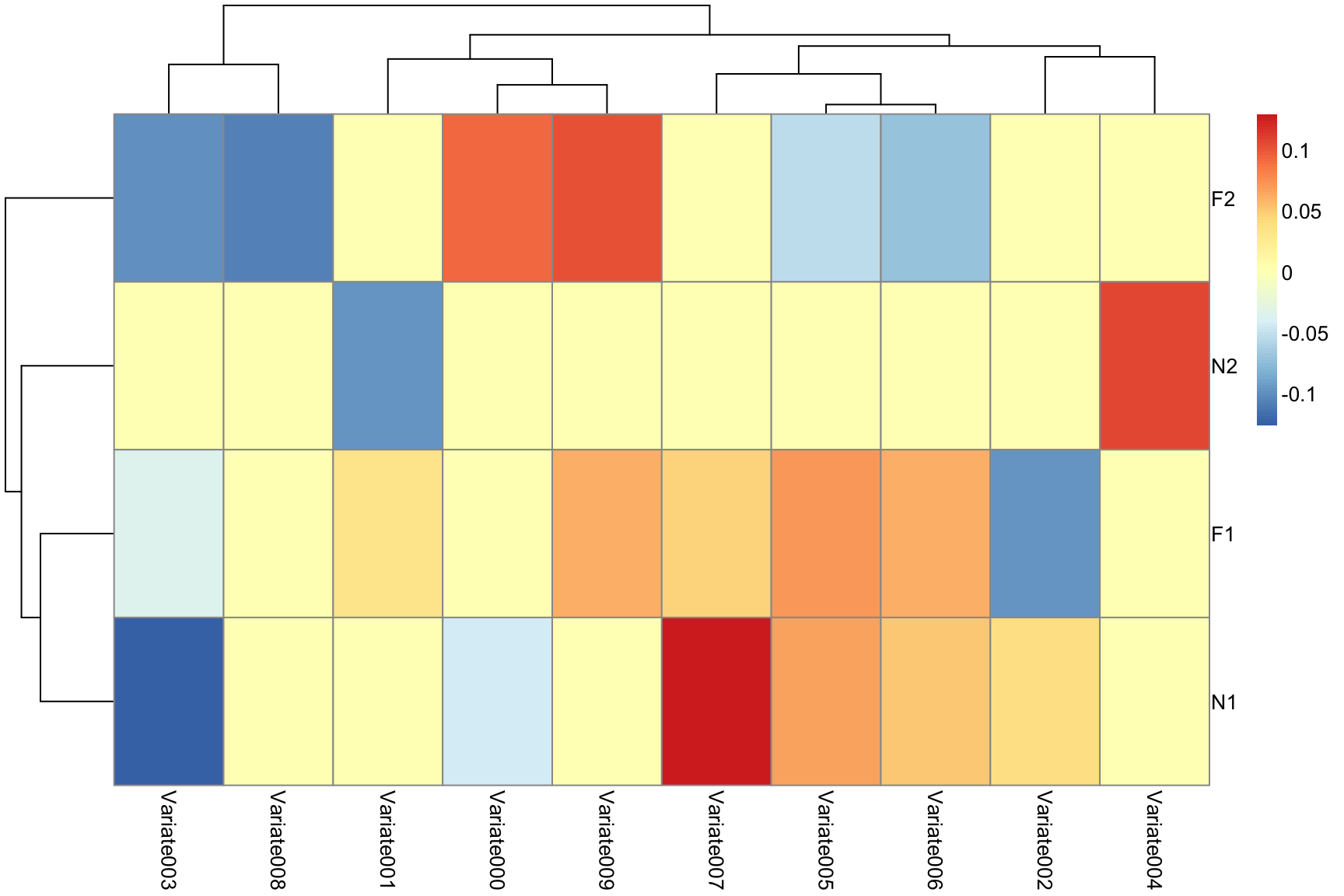

plot of chunk sccanpredictorclass2

Conclusions

With the current RKRNS, one may:

  • Exploit R functionality with BOLD data

  • Estimate HRFs and event-wise betas

  • Use feature selection based on effect sizes

  • Employ dimensionality reduction through eigenanatomy or SCCAN

  • Use relatively few low-dimensional predictors for decoding

  • Interpret multivariate results intuitively

  • Allows us to exploit prior anatomical labels ….

  • or conceptions about what anatomy the decoding should be driven by?

The package needs evaluation at this level of detail on real data.

See RKRNS for all source code and documentation and RKRNS-talk for html slides.

Real data processing with RKRNS

Motion correction

To motion correct your data, one might run:

# get an average image
averageImage <- getAverageOfTimeSeries( boldImage )
motionCorrectionResults <- motion_correction(boldImage, 
   fixed = averageImage, moreaccurate = 0 )

Set the moreaccurate flag to 1 or 2 for usable (not test) results. You might also estimate FD and DVARS from these results. One might use antsPreprocessfMRI to get these directly. Note, however, to turn this function’s frequency filtering off if you want to do decoding.

FD and DVARS

hey hey …

References