apples and oranges …

initialization

apples and oranges …

RGB affine

apples and oranges …

RGB deformable registration - i.e. registration on color

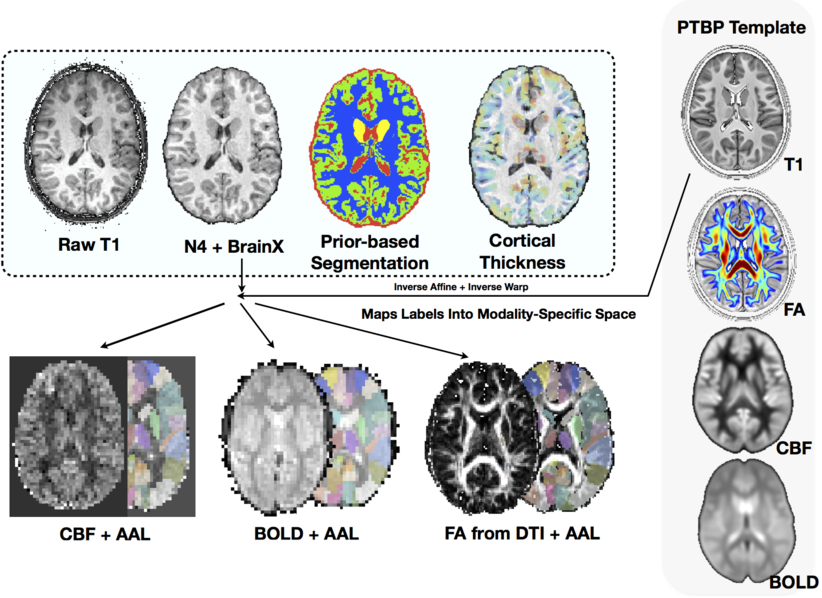
ANTs is open to different image types, multiple modalities, anatomical regions, segmentation priors, etc.

ANTs & Neuroscience

We need statistical image analysis
at several scales in modern neuroscience

• Macro: in vivo structural and functional MRI

• Micro: high-resolution post-mortem MRI links with in vivo MRI

• Nano: neuron reconstruction …

• Solutions that are consistent across these scales have the potential to build multi-scale feature sets or templates and provide new insights into brain structure and function

• E.g. Parcellation constraints based on histology, tractography, function …

• Statistical definitions of anatomy/pathology?

• Reinvention of these solutions within each lab … can we mitigate this?

• Reduce, reuse, recycle …

ANTs Lineage

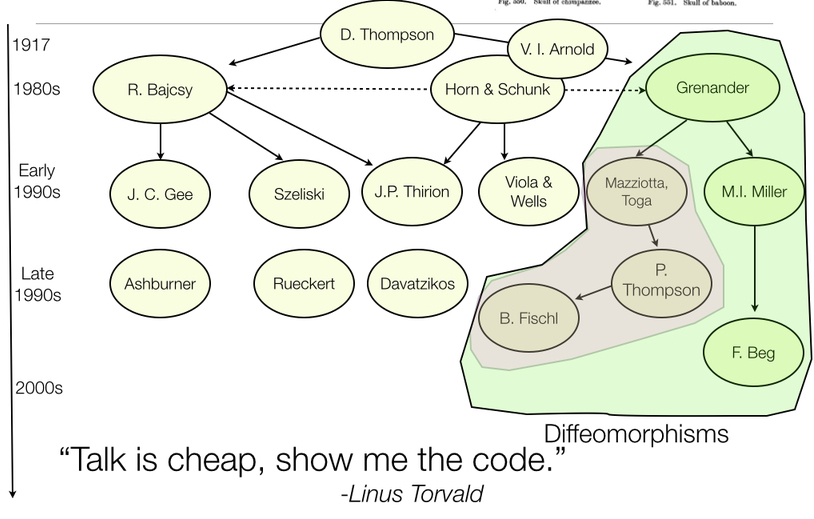
References: Horn and Schunck (1981), Gee, Reivich, and Bajcsy (1993), Grenander (1993), Thompson et al. (2001), Miller, Trouve, and Younes (2002), Shen and Davatzikos (2002), Arnold (2014), Thirion (1998), Rueckert et al. (1999), Fischl (2012), Ashburner (2012)

Diffeomorphisms

plausible physical modeling of large, invertible deformations

“differentiable map with differentiable inverse”

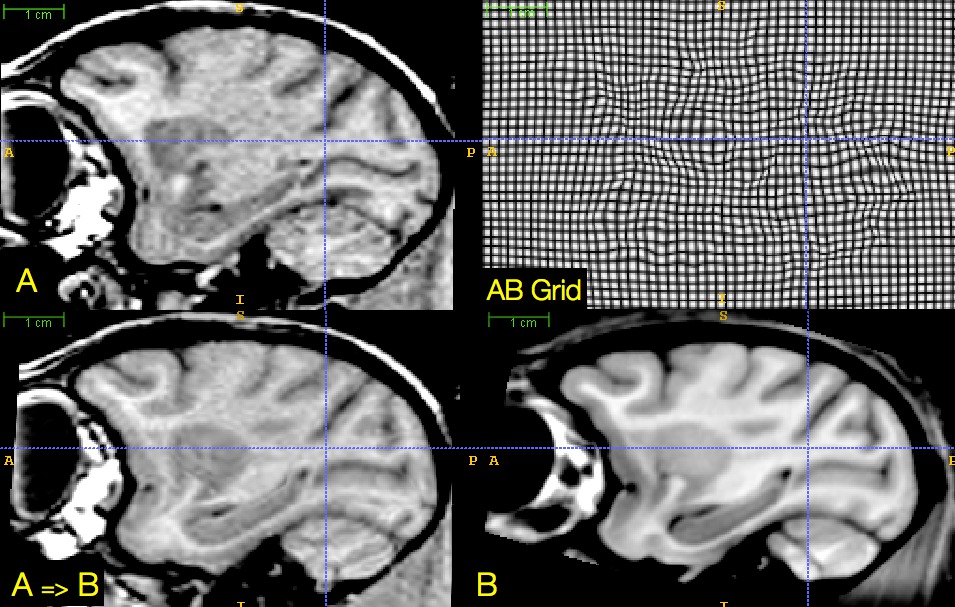
Fine-grained and flexible maps

ANTs: Beyond Registration

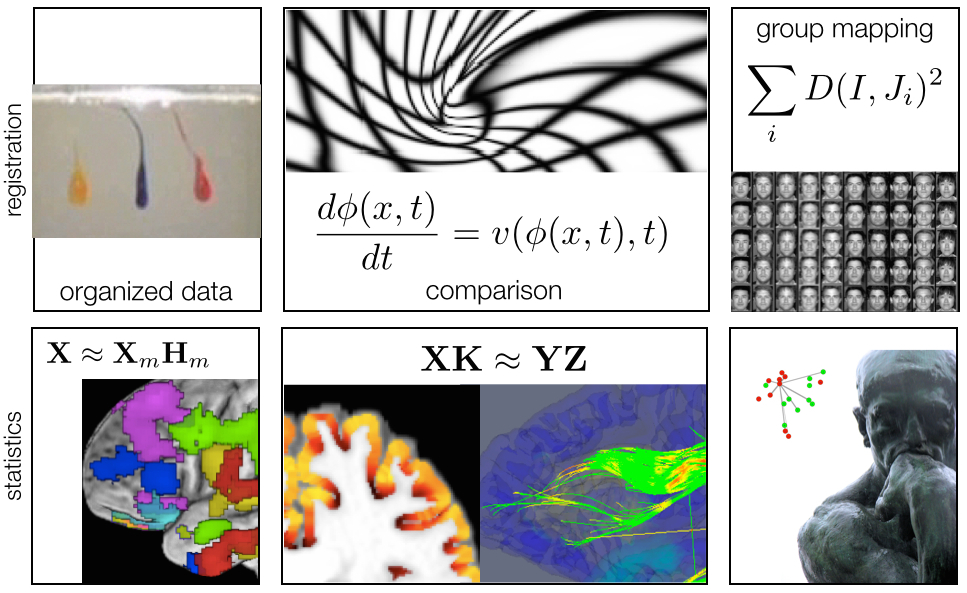
Atropos segmentation, N4 inhomogeneity correction, Eigenanatomy, SCCAN, Prior-constrained PCA, and atlas-based label fusion and MALF (powerful expert systems for segmentation)

but this talk focuses on the core registration functionality that is critical to the applications above

Founding developers

Long-term collaborators

\(+\) neurodebian, slicer, brainsfit, nipype, itk and more …

General purpose library for multivariate image registration, segmentation & statistical analysis tools

• 170,000+ lines of C++, 6\(+\) years of work, 15+ collaborators.

• Generic mathematical methods that are tunable for application specific domains: no-free lunch

• Deep testing on multiple platforms … osx, linux, windows.

• Several “wins” in public knock-abouts ( Klein 2009, Murphy 2011, SATA 2012 and 2013, BRATS 2013, others )

    An algorithm must use prior knowledge about a problem 
    to do well on that problem 

Definitions

• Registration \(=\) estimate an “optimal” geometric mapping between image pairs or image sets (e.g. Affine)

• Similarity \(=\) a function relating one image to another, given a transformation (e.g. mutual information)

• Diffeomorphisms \(=\) differentiable map with differentiable inverse (e.g. “silly putty”, viscous fluid)

• Segmentation \(=\) labeling tissue or anatomy in images, usually automated (e.g. K-means)

• Multivariate \(=\) using many voxels or measurements at once (e.g. PCA, \(p >> n\) ridge regression)

• Multiple modality \(=\) using many modalities at once (e.g. DTI and T1 and BOLD)

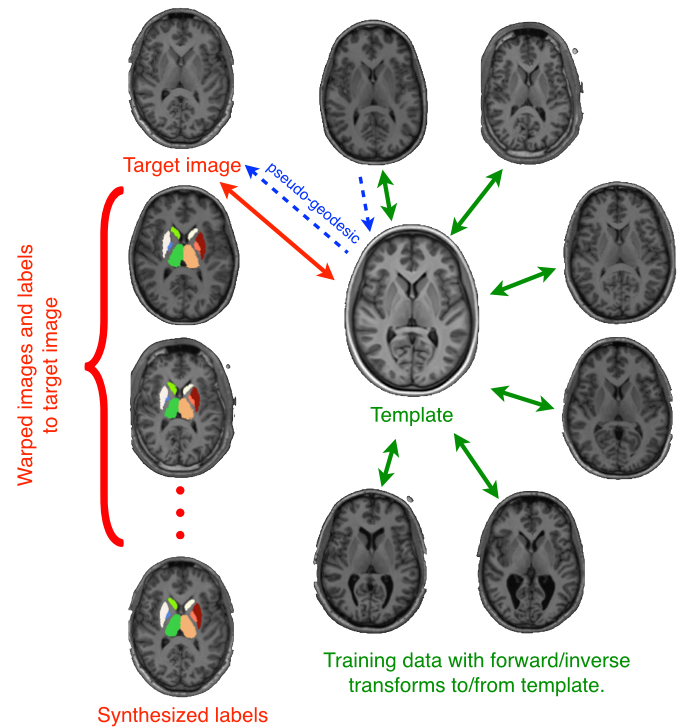
• MALF: multi-atlas label fusion - using anatomical dictionaries to label new data

• Solutions to challenging statistical image processing problems usually need elements from each of the above

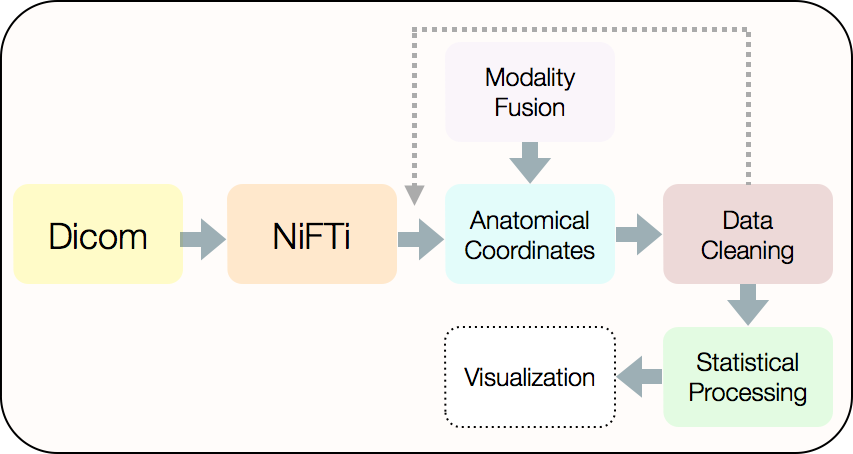
The Technical Framework

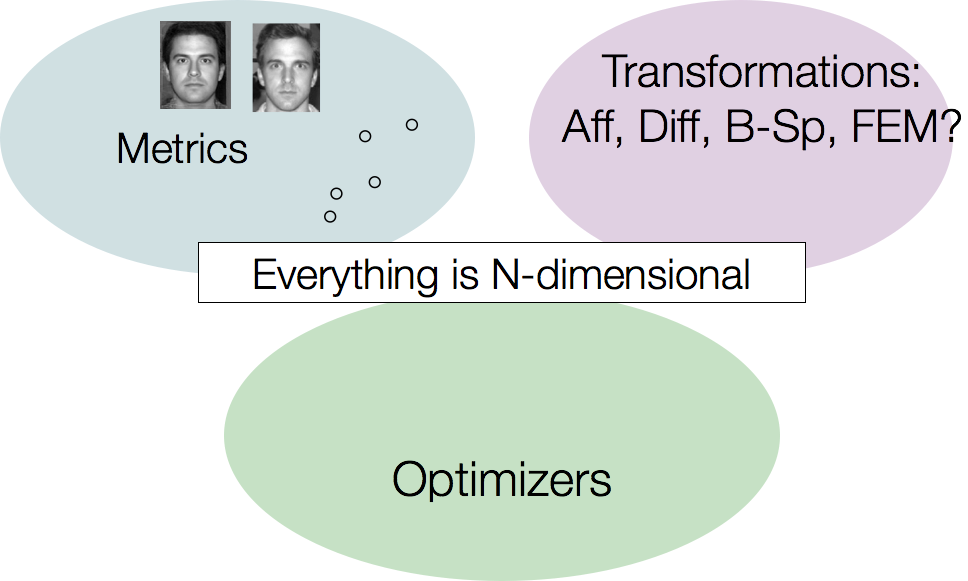
… and most of it multivariate.

ANTs Nomenclature / Standards

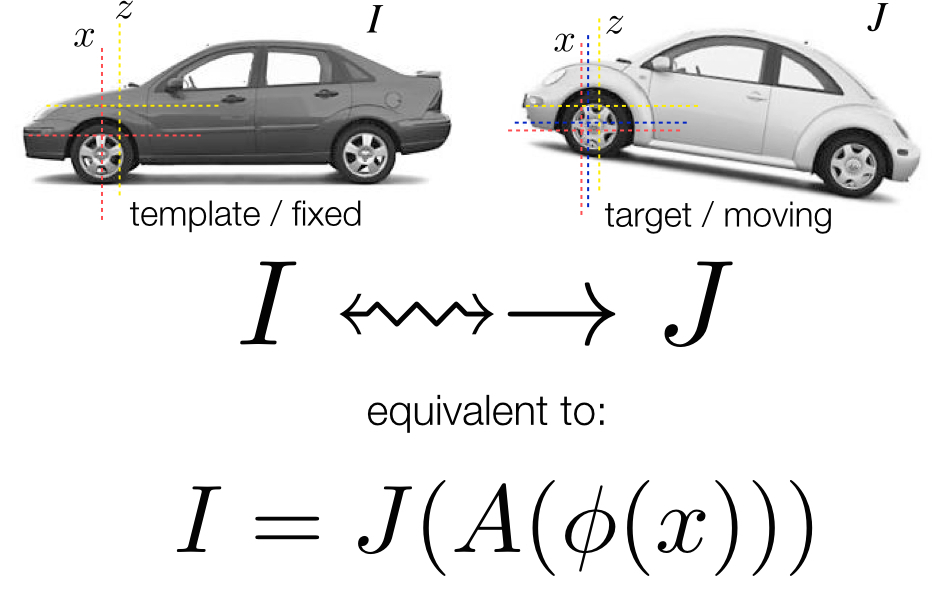
ANTs Nomenclature / Standards

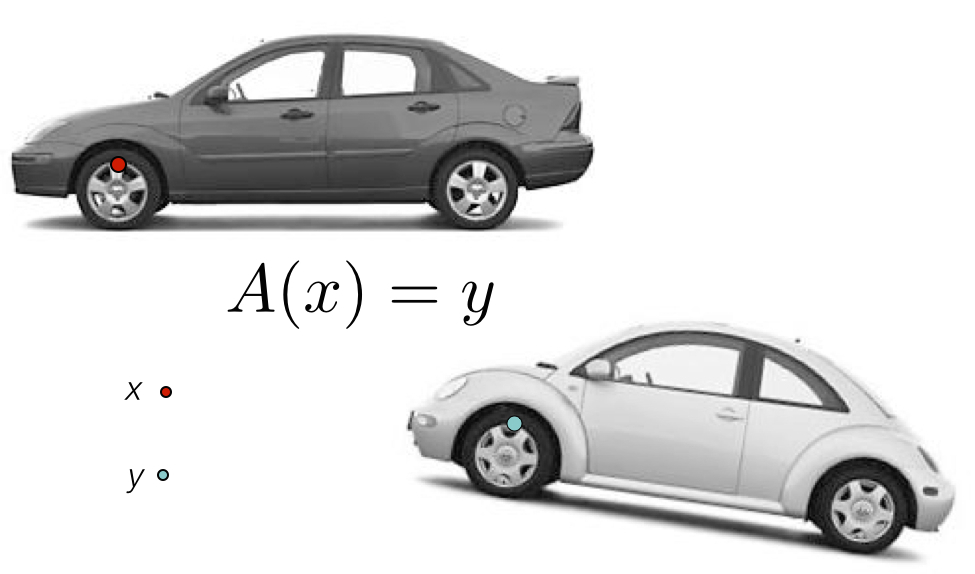
ANTs Nomenclature / Standards

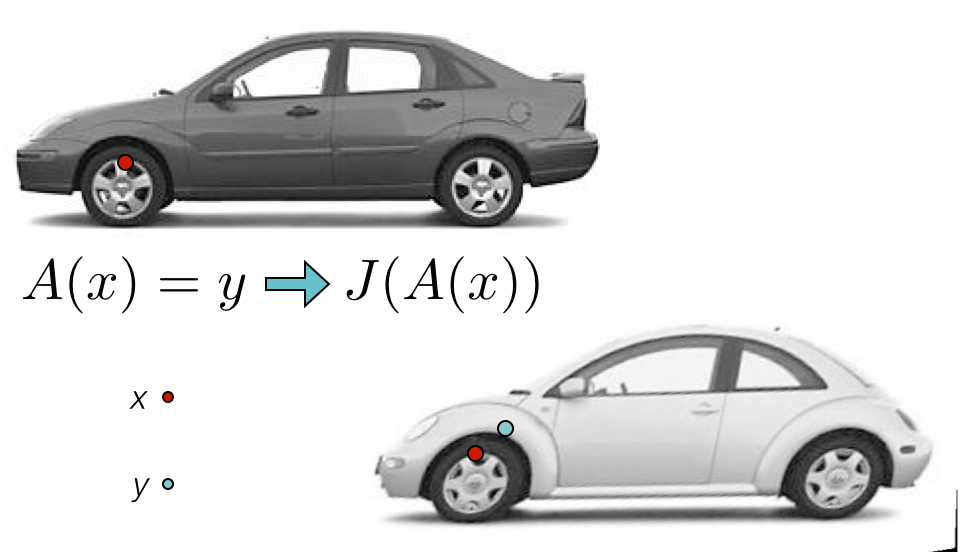
ANTs Nomenclature / Standards

The optimization problem

Find mapping \[ \color{red}{ \phi(x,p) \in \mathcal{T} }\] such that

\[ \color{red}{ M(I,J,\phi(x,p)) } \] is minimized

Must select both metric \(\color{red}{M}\) and transformation \(\color{red}{\mathcal{T}}\)

… in addition to optimizer and the problem’s resolution

Discussed in more detail in this frontiers paper

The A-team of similarity metrics

\[ \| I - J \| ~~~~~~~~~~~~~~~~~~~ \frac{< I, J >}{\|I\|\|J\|} ~~~~~~~~~~~~~~~ p(I,J) log \frac{p(I,J)}{p(I)p(J)}\]

all metrics may be computed from sparse or dense samples and used with low or high-dimensional transformations

our research on similarity metrics for brain registration

SyN for optimization symmetry

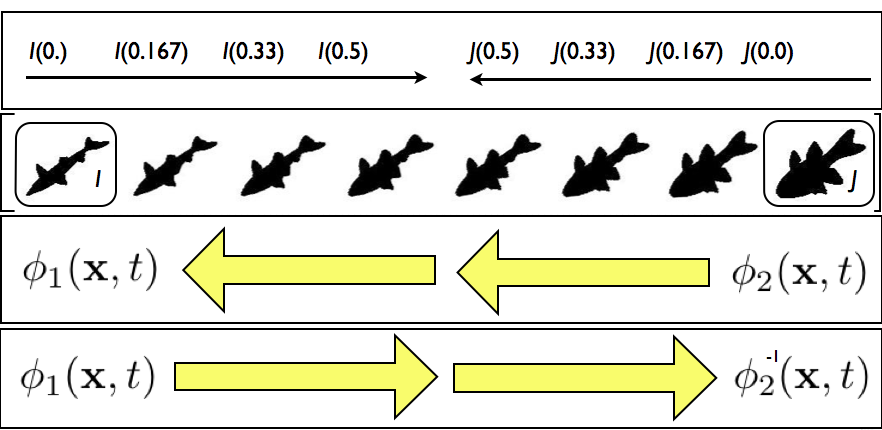Images deform symmetrically along the shape manifold. This eliminates bias in the measurement of image differences.

SyN (link) Example

SyN movie

Concatenated transformation \(+\) metric stages are necessary in real data

0. Initialize the mapping ( more on this later )

1. Start with a rigid transformation: \(I(x) \approx J(R(x))\) s.t. negative \(MI\) is minimized

2. Follow by an affine transformation: \(I(x) \approx J(R(A(x)))\) s.t. negative \(MI\) is minimized with fixed \(R\)

3. Finally, a diffeomorphism: \(I(x) \approx J(R(A(\phi(x))))\) s.t. \(k\)-neighborhood correlation \(CC_k\) is minimized with fixed \(R, A\)

4. Output the composite transform \(A \circ R\) as a matrix transformation and \(\phi\) and \(\phi^{-1}\) as deformation fields.

standard in recommended antsRegistration application scripts

Minimizing interpolations

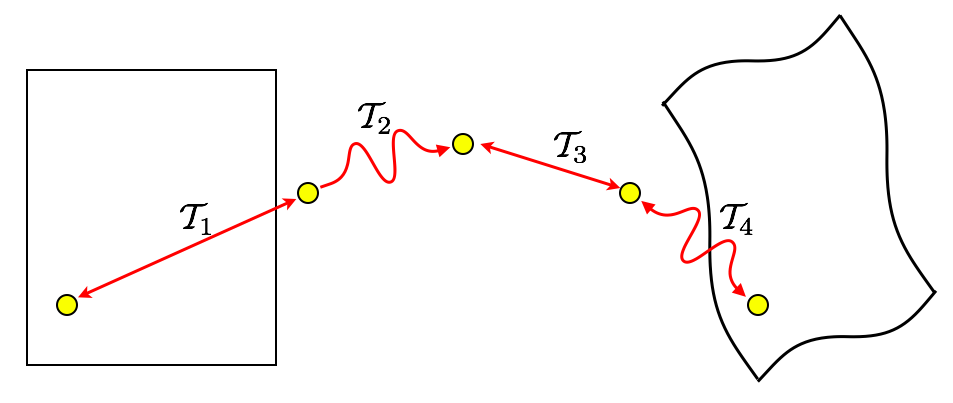
\(\mathcal{T}_{total} = \mathcal{T}_1 \circ \mathcal{T}_2 \circ \mathcal{T}_3 \circ \mathcal{T}_4\)

To avoid compounding interpolation error with the concatenation of transformations, ANTs never uses more than a single interpolation.

We ported many of these ideas into the Insight ToolKit
as part of its V4 reboot!

Registration benefits from
optimal sampling strategy

• sampling for both the metric and the transformation

• impacts scalability, memory, optimization accuracy, speed, robustness …

• could be done optimally with massive improvements in performance
  • but needs investment in order to achieve “dream” registration scenario

• important for new schemes that elect solutions from anatomical or transformation dictionaries

• overall, relatively little translational work on this important problem in biomedical imaging

Sampling & feature selection: Multi-start

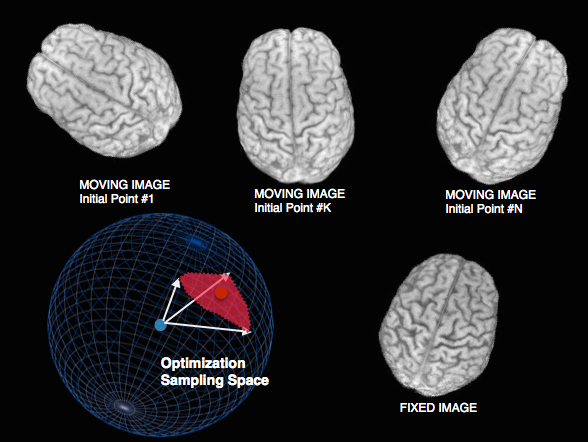
Theoretical guarantee of global optimum: improves local optimizers.

Default in antsCorticalThickness pipeline and FSL.

Sampling & feature selection: Biomedical imagery

Initial configuration of data

Sampling & feature selection: Biomedical imagery

Automatic feature selection

Sampling & feature selection: Biomedical imagery

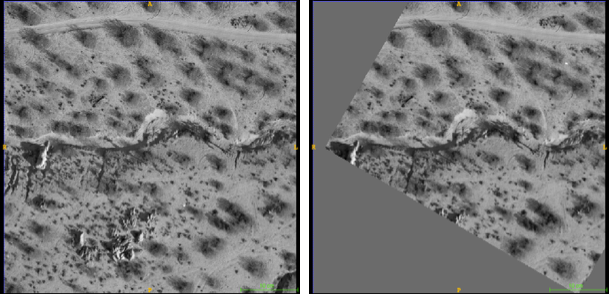
Resampling allows comparison & slide alignment and
validates the feature selection

Dramatic reduction in computation time / memory requirements

Sampling & feature selection: Lesioned brains

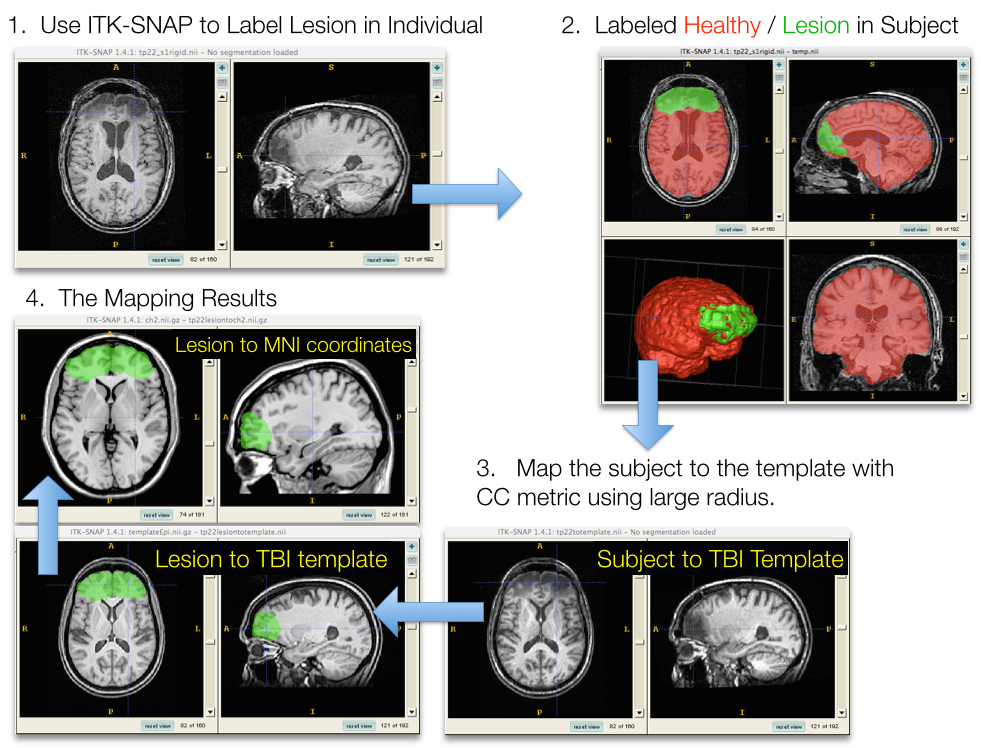
Sampling & feature selection: Summary

• we exploit these strategies to:
  • accelerate
  • focus
  • validate

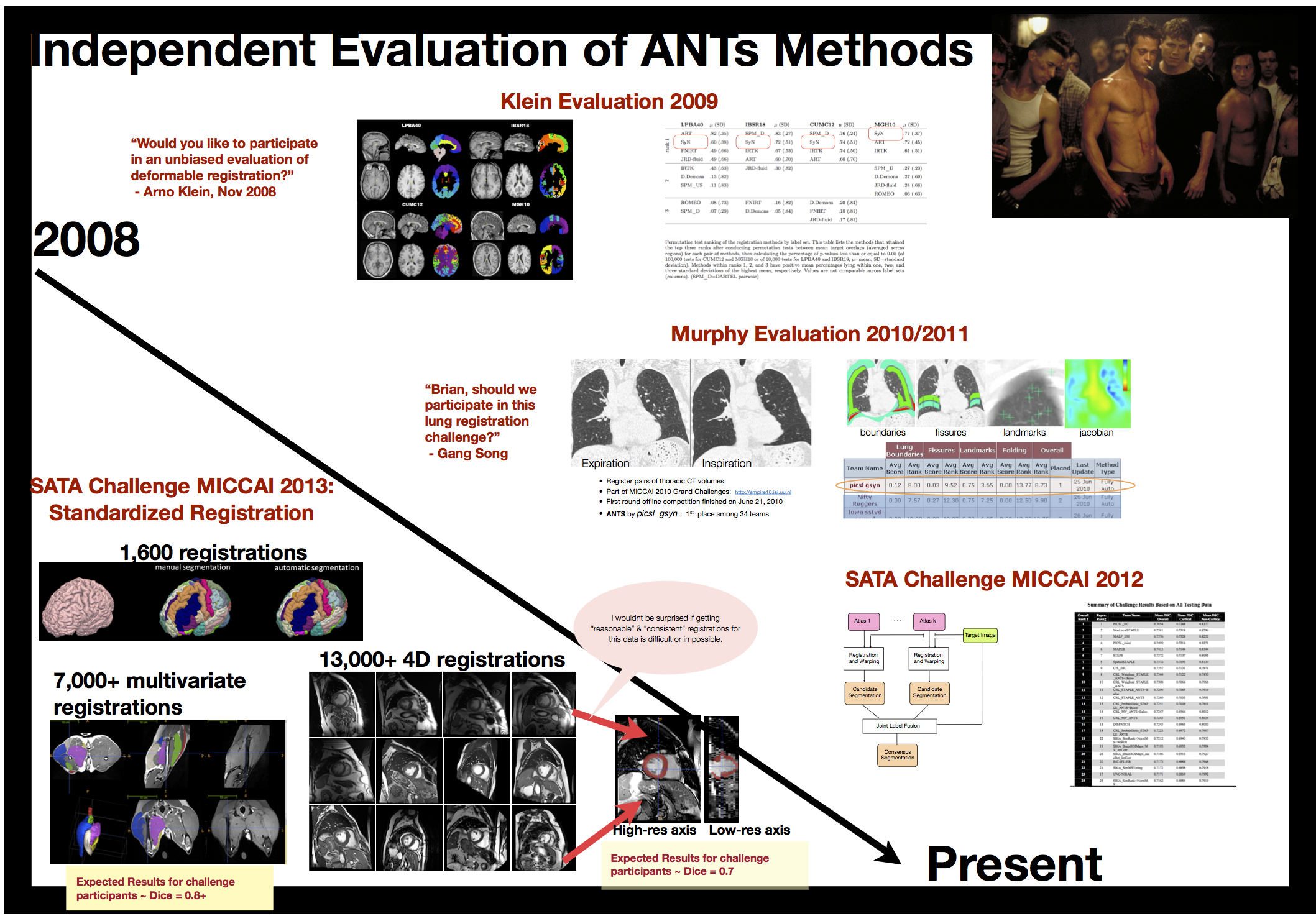
Anatomical dictionaries

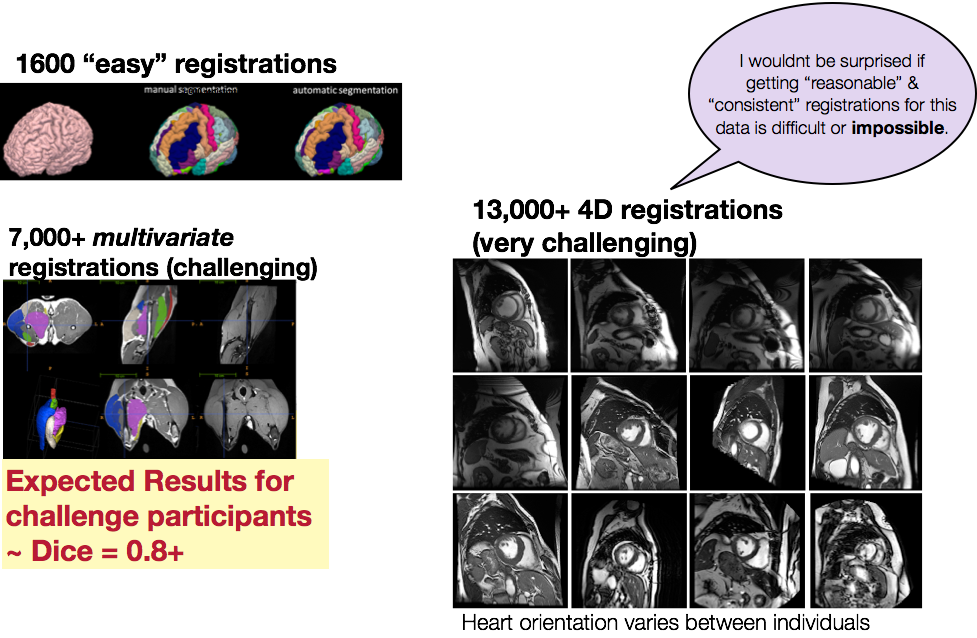
we provided the standard registration results for \(>\) 20,000 image pairs at SATA 2013

label fusion (link)

Multiple metrics improve performance

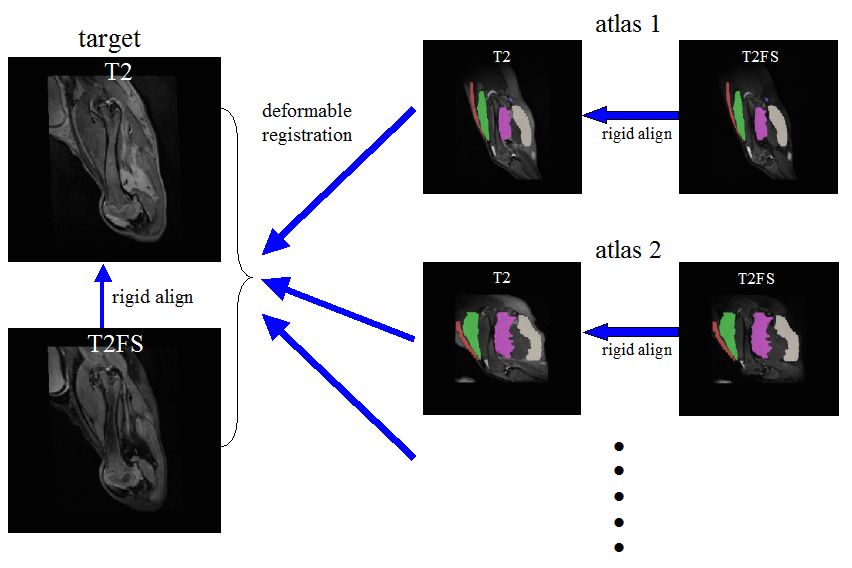
to our knowledge, ANTs is the only freely available system that can solve this problem in a fully multivariate manner.

Hongzhi Wang won the “walk in the park” award for this work …

Brain templates as high-dimensional averages

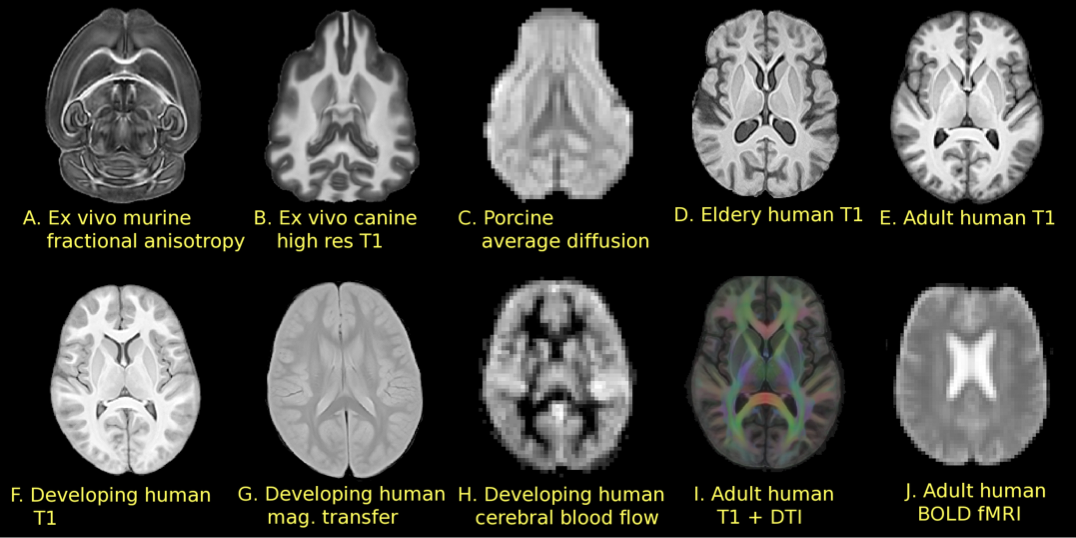
SyGN - templates and averages in deformation space

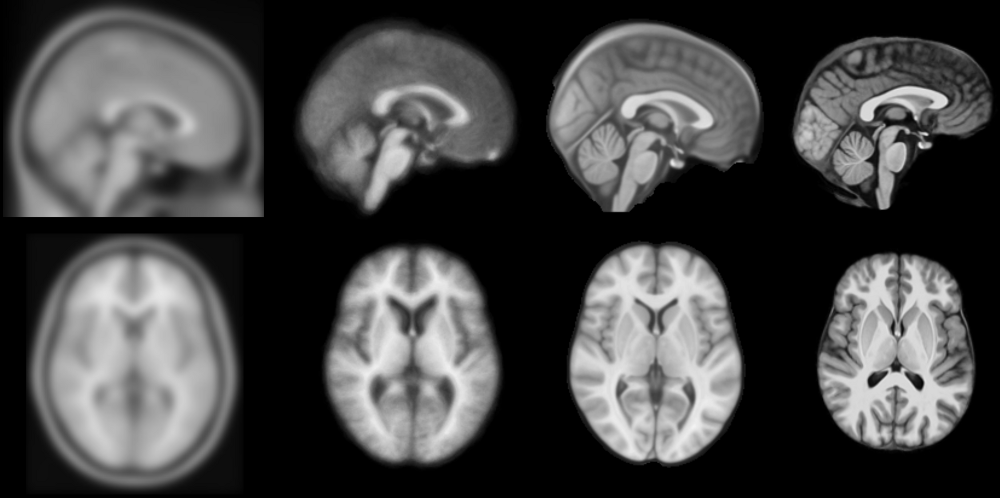from miykael

geodesic image averages

optimal templates 2

canine template

chimpanzees

Statistics in deformation space

AIBS movie

Average Republican and Democratic congressmen

congress

ANTs versus Freesurfer:
Quantifying life span brain health

• Freesurfer is the historical standard for measuring cortical thickness

• instead of using surfaces to measure cortical thickness, we use the image space DiReCTly

• see this section of a different talk

• and this “big data” paper: Large-scale evaluation of ANTs and FreeSurfer cortical thickness measurements

• comparison of prediction from automated cortical thickness measurement from 4 public datasets

• \(>\) 1200 subjects, age 7 to over 90 years old

• hint: ANTs thickness measurements have higher prediction accuracy relative to Freesurfer ( implying we extract more information from the data )

• ANTs methods consistently improve statistical power eigenanatomy, syn, itkv4 … also, see Schwarz CG, et al. re: TBSS and related work in fMRI Miller, PNAS, Azab, et al in Hippocampus.

multivariate statistical fields arise from fused modalities

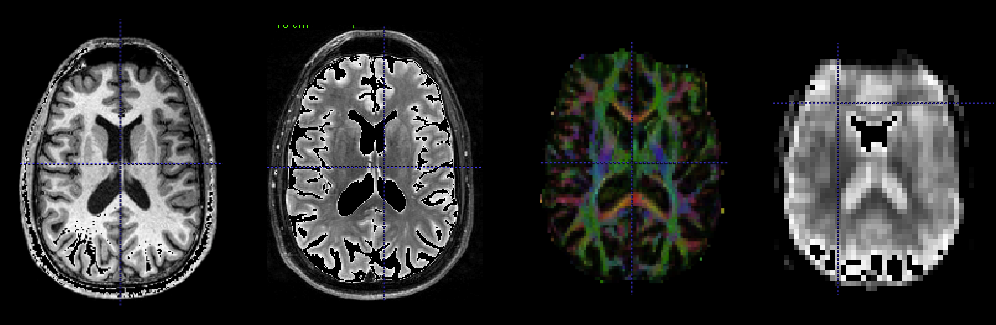
Many opportunities for statistical advancements

Scientific Data 2014

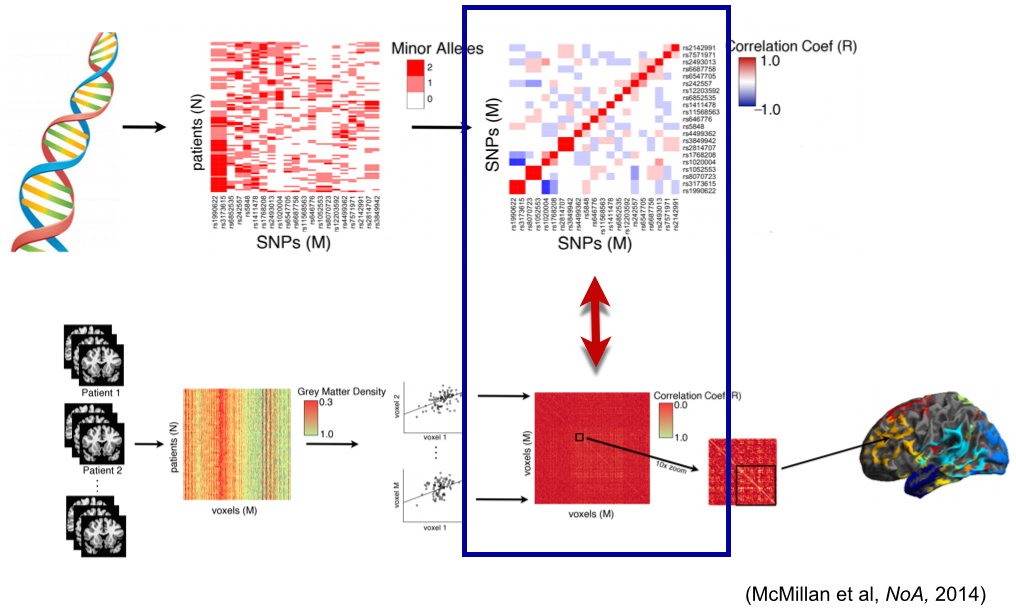
“Network” of predictors for age

…

ITK+ANTs+R = ANTsR

Agnostic statistics

McMillan et al.

A Quick ANTsR example

This is an executable ANTsR code block - N-dimensional statistics to go with our N-dimensional image processing software!

library(ANTsR)
dim<-2
filename<-getANTsRData('r16')
img<-antsImageRead( filename , dim )
filename<-getANTsRData('r64')
img2<-antsImageRead( filename , dim )
mask<-getMask(img,50,max(img),T)
mask2<-getMask(img,150,max(img),T)
nvox<-sum( mask == 1 )
nvox2<-sum( mask2 == 1 )

The brain has 17395 voxels …

A Quick ANTsR example

Simulate a population morphometry study - a “VBM” …

simnum<-10
imglist<-list()
imglist2<-list()
for ( i in 1:simnum ) {
  img1sim<-antsImageClone(img)
  img1sim[ mask==1 ]<-rnorm(nvox,mean=0.5)
  img1sim[ mask2==1 ]<-rnorm(nvox2,mean=2.0)
  img2sim<-antsImageClone(img2)
  img2sim[ mask==1 ]<-rnorm(nvox,mean=0.20)
  imglist<-lappend(imglist,img1sim)
  imglist2<-lappend(imglist2,img2sim)
}
imglist<-lappend( imglist, imglist2 )
mat<-imageListToMatrix( imglist, mask )
DX<-factor( c( rep(0,simnum), rep(1,simnum) ) )
mylmresults<-bigLMStats( lm( mat ~ DX ) )
qvals<-p.adjust( mylmresults$pval.model ) 

The minimum q-value is 3.0363 × 10^-5 …

Visualize the histograms of effects

whichvox<-qvals < 1.e-2
voxdf<-data.frame( volume=c( as.numeric( mat[,whichvox] ) ), DX=DX )
ggplot(voxdf, aes(volume, fill = DX)) + geom_density(alpha = 0.2)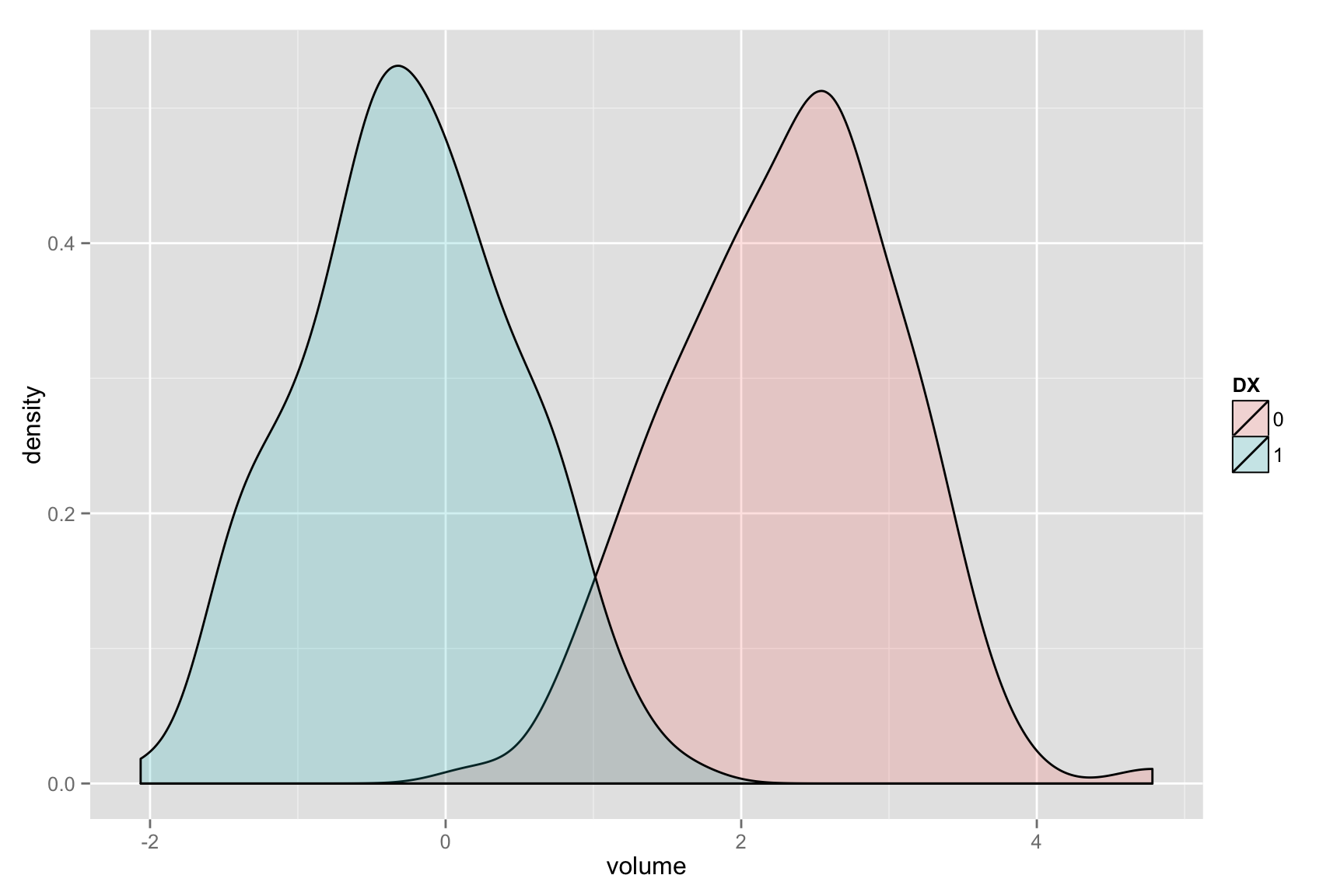

Visualize the anatomical distribution

plotANTsImage(img,functional=list(betas),threshold=thresh,
  outname=ofn)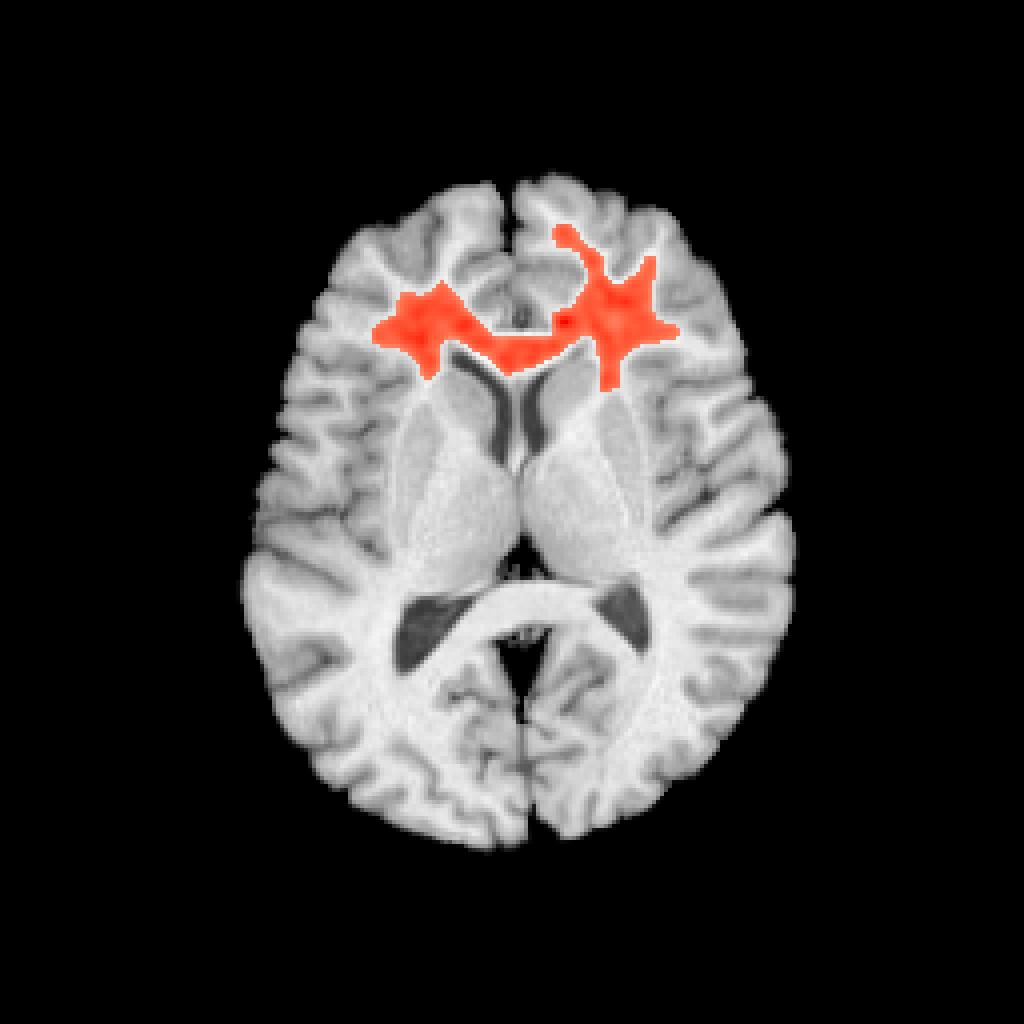

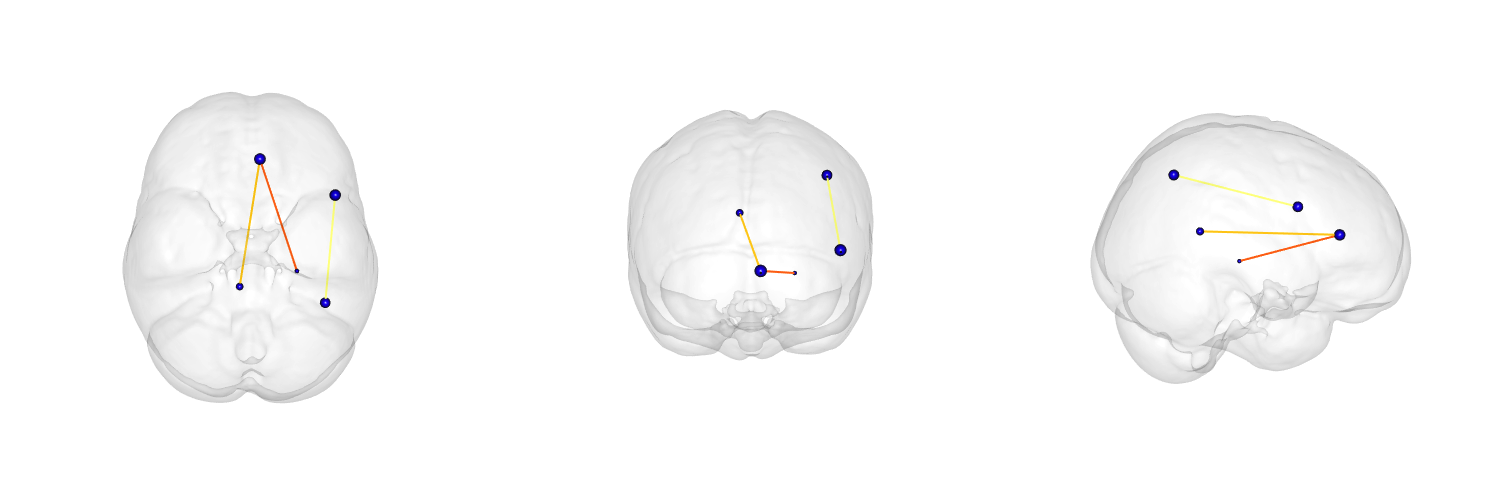
Network visualization

see ?plotBasicNetwork

The power of ANTs \(+\) R \(\rightarrow\)
Reproducible imaging science

… used in “Sparse canonical correlation analysis relates network-level atrophy to multivariate cognitive measures in a neurodegenerative population” and several upcoming …

Can we customize these methods for a challenging multivariate segmentation problem with clinical relevance?

Automated tumor segmentation from multiple MRI

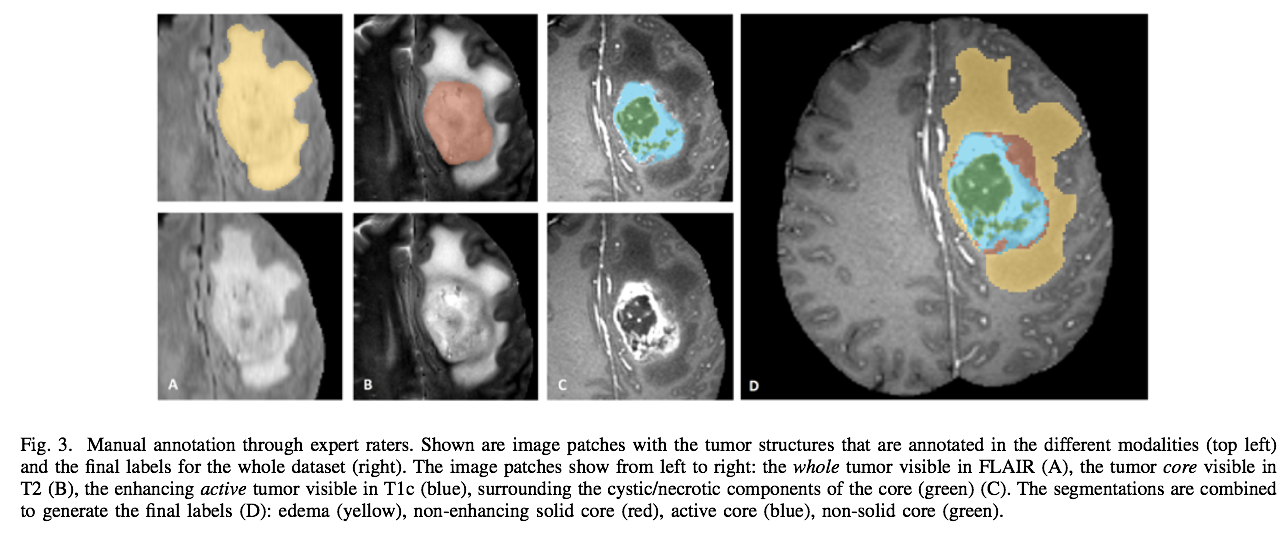
General theory tunable to specific domains: no-free lunch

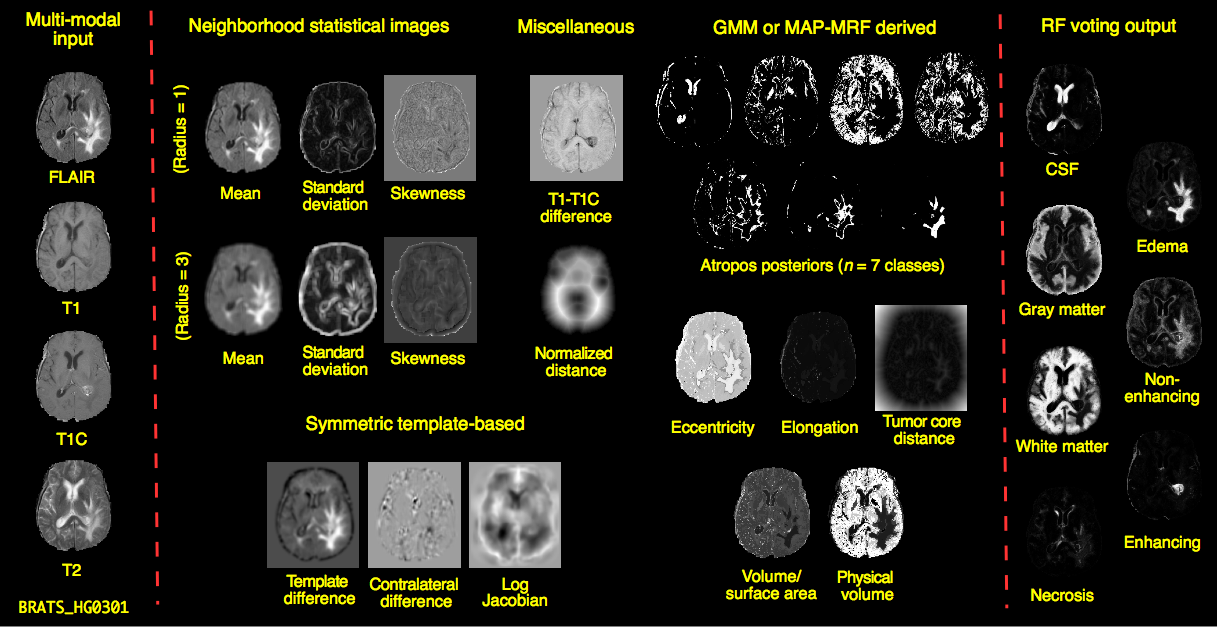
BRATS 2013 Challenge won with ANTsR

Can we address subtle questions in brain and cognition via imaging-specific dimensionality reduction?

Eigenanatomy & SCCAN

ANTsR \(\rightarrow\) new insight
via better analytics

Good software should fade into the background … however …

As is common in science, the first big breakthrough in our understanding … [came from] an improvement in measurement.

> Daniel Kahnemann, Thinking, Fast and Slow (2011)

Recap

• Powerful, general-purpose, well-evaluated registration and segmentation.

• Differentiable maps with differentiable inverse \(+\) statistics in these spaces

• Evaluated in multiple problem domains via internal studies & open competition

• Borg philosophy: “best of” from I/O, to processing to statistical methods

• Open source, testing, many examples, consistent style, multiple platforms, active community support …

• Integration with R \(+\) novel tools for prediction, decoding, high-to-low dimensional statistics.

• Collaborations with neurodebian, slicer, brainsfit, nipype, itk and more …

Challenges: Computational and Scientific

• Scalability
  • need to fuse feature selection methods with transformation optimization
  • need to leverage existing ITK streaming infrastructure in application level tool
• Domain expertise: Customizable for specific problems but sometimes not specific enough
• “Plausible physical modeling …” - this should vary per problem … but doesn’t.
  • a fabulous project would be to resolve this issue at a large-scale e.g. for reconstructing neurons, measuring white matter elaboration …
  • our prior FEM work is one potential solution
• Rapid development: colleagues still need familiarity with compilation for latest ANTs features
• Latest theoretical advances in registration not yet wrapped for users
• Need more Documentation & testing …

Tools you can use for imaging science

• Core developers: B. Avants, N. Tustison, H. J. Johnson, J. T. Duda

• Many contributors, including users …

• Multi-platform, multi-threaded C++ stnava.github.io/ANTs

• Developed in conjunction with http://www.itk.org/

• R wrapping and extension stnava.github.io/ANTsR

• rapid development, regular testing \(+\) many eyes \(\rightarrow\) bugs are shallow

What is and is not
image registration

not registration

Voodoo in voxel-based analysis

logical circularity VBA

Instrumentation bias in the use and evaluation of software

Instrumentation bias in the use and evaluation of software